数学建模-Matlab学习笔记(十三)图论
本文最后更新于:December 3, 2021 pm
MATLAB(矩阵实验室)是第四代高层次的编程语言和交互式环境数值计算,可视化和编程。由美国MathWorks公司开发的一种编程语言。用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。拥有众多的内置命令和数学函数,可以帮助您在数学计算,绘图和执行数值计算方法。
目录
一.画网络图
Matlab有一个自带的biography类型,可以直接画图论关系图。在Matlab中一般用稀疏矩阵(sparse函数)。
1 | |
其中,R和C分别表示节点,W表示对应两节点之间的权值。(R和C分别表示节点坐标x,y的标量,W表示对应两节点之间的边权值。)注意:sparse函数会生成一个m*n对double型矩阵,m是R中最大的数字,n是C中最大的数字。如果其值不相同,那么生成的矩阵将不是方阵,而所有的图论算法操作的矩阵都是方阵,所以在R和C和W的最后添加了8 7 0三个数字,来保证生成方阵。如果R C中出现重复边,会将其权值相加。所以最后在W里写0,不影响边权值。
1 | |
其中biography为生成一个biography object ,[]中为节点名称 默认为Node1 ,‘ShowW' ‘ON' 表示显示权值 类似的有'ShowArrows' ‘ON’为显示箭头。
二.图涂色
1 | |
效果如图:
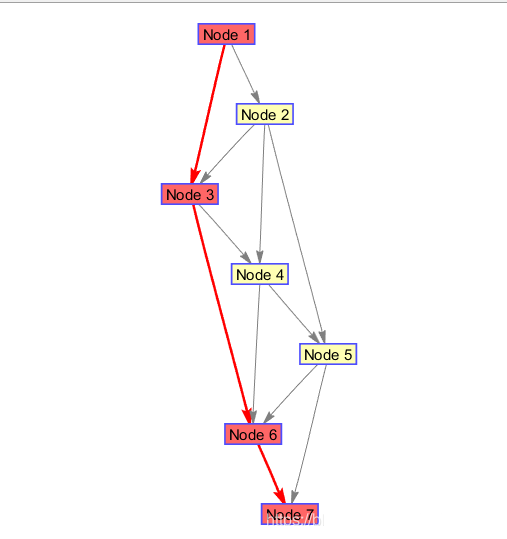
1 | |
效果如图:
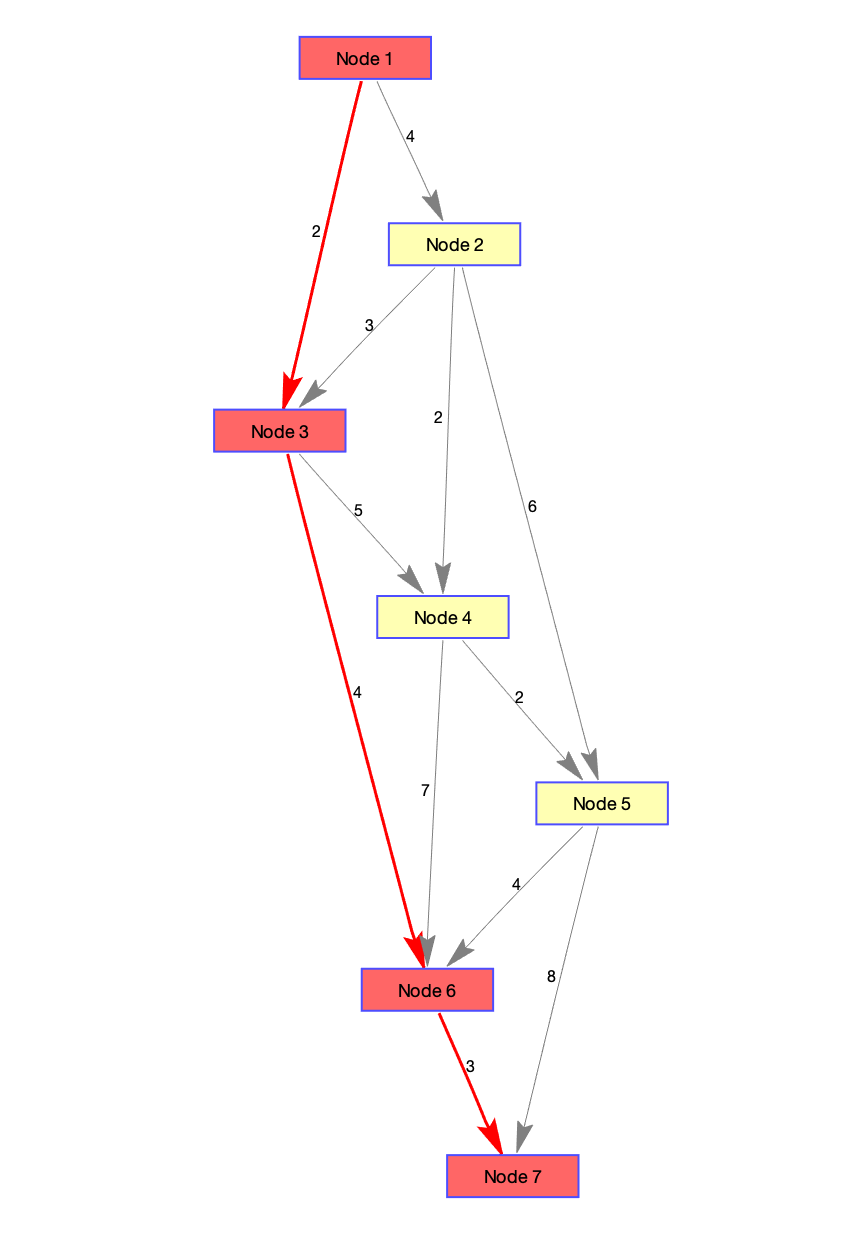
二.图论工具箱
1.最短路
1.1 指定点对
- 功能
求指定的一对顶点间的最短距离和最短路径。
- 使用方法
1 | |
其中v1,v2为两点。返回的dist为路径长,path为路径。
- 使用一:
1 | |
- 使用二:
1 | |
1.2 任意点对
- 功能
求图中所有顶点对之间的最短路径。
- 使用格式
1 | |
如果想要生成无向图,需要这样操作:UG=tril(G+G');就是把G和自己的转置G’加起来再求等价变换得到的下三角矩阵。
DirectedValue属性:True(有向图,默认),false(无向图)。
WeightsValue属性:Weightvalue属性一般不用指定,函数graphallshortestpath函数默认从稀疏矩阵G中获取。
Dist输出参数:输出[dist]是一个N * N的矩阵,每一个元素代表两点之间最短距离,对角线上的元素总为零,不在对角线上的零表示起点和终点的距离为零,inf值表示没有路径。
2.最小生成树
- 功能
在图中找最小生成树
- 使用格式
1 | |
- 参数:Tree(一个代表生成树的稀疏矩阵);Pred(包含最小生成的祖先节点的向量);G(稀疏矩阵);R(根节点,取值为1到节点数目);Method(可以选择‘Kruskal’,’Prim’等算法)。
使用:
1 | |
3.最大流
- 功能
计算有向图的最大流
- 使用格式
1 | |
- 参数:输入参数G(N * N的稀疏矩阵);输入参数SNode(起点);输入参数TNcode(目标点);CapacityValue属性(每条边自定义容量的列向量,默认从G中获取);MethodValue属性(可以取‘Edmonds’和‘Goldberg’算法);输出参数MaxFlow(网络最大流);输出参数FlowMatrix(每条边数据流的值所组成的稀疏矩阵);输出参数cut(连接起点与目标点的逻辑向量,如果有多个解时,Cut是一个矩阵)。
4.图的遍历
- 功能
从某一个顶点出发,遍历图中所有的顶点。可以用来判断一个图是否连通。
- 使用格式
1 | |
- 参数:G(有向图的稀疏矩阵);S(起始节点);Disc(节点索引向量);Pred(祖先节点索引向量)。
Methodvalue表示遍历方法:默认为“深度优先遍历”。可选BFS、DFS。
Depthvalue表示遍历深度值:表示图G中指定搜索深度的节点的整数。默认值是Inf(无穷大)。
待更新函数
| 函数名 | 功能描述 |
|---|---|
graphconncomp |
找无向图的连通分支,或有向图的强弱连通分支 |
graphisdag |
测试有向图是否含有圈,不含圈返回1,否则返回0 |
graphisomorphism |
确定两个图是否同构,同构返回1,否则返回0 |
graphisspantree |
确定一个图是否是生成树,是返回1,否则返回0 |
graphpred2path |
把前驱顶点序列变成路径的顶点序列 |
graphtopootder |
执行有向无圈图的拓扑排序 |
graphtraverse |
求从一顶点出发,所能遍历图中的顶点 |
本文作者: 墨水记忆
本文链接: https://tothefor.com/DragonOne/1598674743.html
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
