算法学习-前缀和与差分详解
本文最后更新于:March 18, 2022 pm
纸上得来终觉浅,绝知此事要躬行。路漫漫其修远兮,吾将上下而求索!知识是经过历史的巨人沉淀下来的,别总想着自己能够快速学会,多花点时间去看看,也许会发现些不同的东西。你能快速学会的、觉得简单的东西,对于别人来说也是一样的。人外有人,天外有天。当努力到达了一定的程度,幸运自会与你不期而遇。
目录
开始之前,推荐先看一下总结。再看内容。也许会帮你更好的理解。
前缀和是指某序列的前n项和,可以把它理解为数学上的数列的前n项和,而差分可以看成前缀和的逆运算。合理的使用前缀和与差分,可以将某些复杂的问题简单化。
1.前缀和
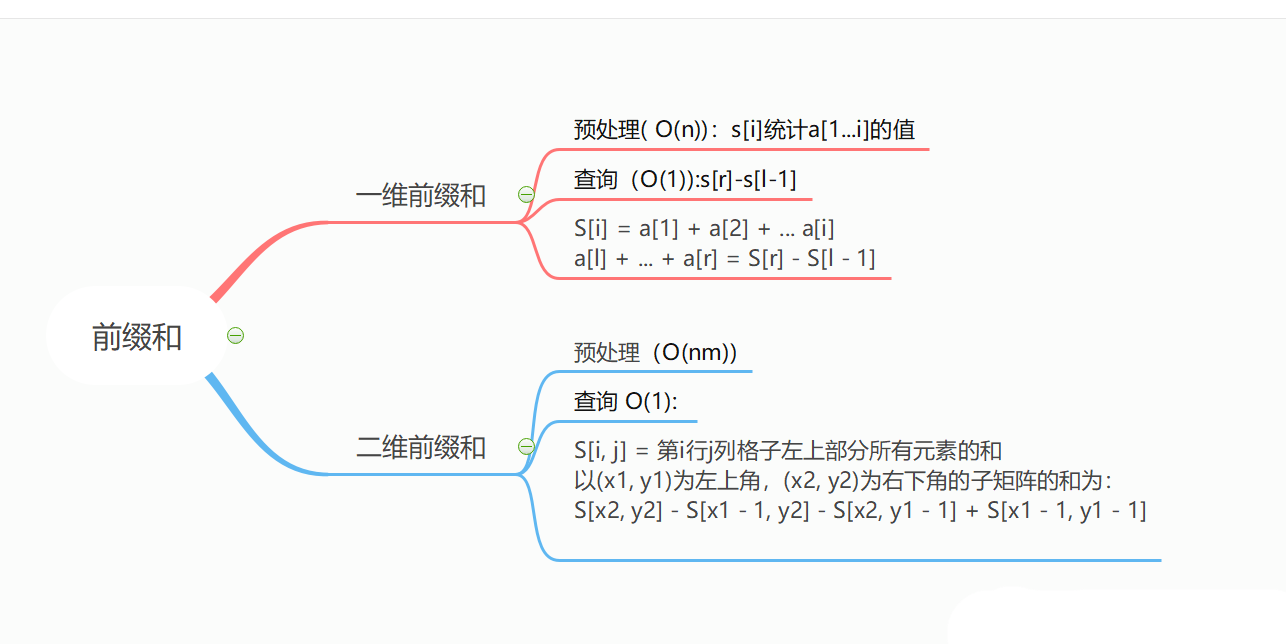
首先,看一个问题:
输入一个长度为n的整数序列。接下来再输入m个询问,每个询问输入一对l, r。对于每个询问,输出原序列中从第l个数到第r个数的和。
这个问题,最容易想到的就是暴力了。但当数大了之后,时间复杂度就比较高了。
1.1 一维前缀和
首先明白两个数组,一个是原数组a,一个是前缀和数组sum。
- 前缀和数组的定义:sum[i]=a[1]+a[2]+a[3]+…+a[i],即为前i个数的和:
假设的是a[1]=1,a[2]=2….a[i]=i。
sum[1]=a[1]; //1
sum[2]=a[1]+a[2]; //3
sum[3]=a[1]+a[2]+a[3]; //6
sum[4]=a[1]+a[2]+a[3]+a[4]; //10
sum[5]=a[1]+a[2]+a[3]+a[4]+a[5]; //15
……
sum[i]=a[1]+a[2]+a[3]+…+a[i]。
假如我们要求[2,5]区间的和,怎么求?看上面列出来的。
是不是直接用sum[5]-sum[1]即可。因为:a[1]+a[2]+a[3]+a[4]+a[5]-a[1]=a[2]+a[3]+a[4]+a[5]。
并且sum[5]=sum[4]+a[5]的。即sum[i]=sum[i-1]+a[i]的。
所以,如果求[l,r]的区间和,则直接用:sum[r]-sum[l-1]即可。
原理
sum[r] =a[1]+a[2]+a[3]+a[l-1]+a[l]+a[l+1]……a[r];
sum[l-1]=a[1]+a[2]+a[3]+a[l-1];
sum[r]-sum[l-1]=a[l]+a[l+1]+……+a[r];
右边会把相同的消掉。如图:

这样,对于每个询问,只需要执行 sum[r]-sum[l-1]。输出原序列中从第l个数到第r个数的和的时间复杂度变成了O(1)。
代码实现:
1 | |
这就是一维前缀和。

1.2 二维前缀和
二维前缀和和一维差不多,二维中的sum存的是一块区域的面积。这里为了方便sum数组就写成s数组了。
还是先看一个问题:
输入一个n行m列的整数矩阵,再输入q个询问,每个询问包含四个整数x1, y1, x2, y2,表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。
二维前缀和的sum数组求法
定义一个二维数组s[][], s[i][j]表示二维数组中,左上角(1,1)到右下角( i,j )所包围的矩阵元素的和。需要注意的是,这里的(1,1)根据自行情况而定。可能有的人是(0,0),或其他的。这里都统一以(1,1)开始。
如图:

其中,紫色面积是指(1,1)到(i,j-1)的矩形面积, 绿色面积是指(1,1)到(i-1, j )的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。
从图中我们很容易看出,整个外围蓝色矩形面积s[i][j] = 绿色面积s[i-1][j] + 紫色面积s[i][j-1] - 重复加的红色的面积s[i-1][j-1]+小方块的面积a[i][j];
所以,得出二维前缀和sum数组的预处理公式:s[i] [j] = s[i-1][j] + s[i][j-1] + a[i] [j] - s[i-1][ j-1]
二维前缀和的区间求法
现在,sum数组已经处理好了。我们来求一下二维的区间和问题。求以(x1,y1)为左上角和以(x2,y2)为右下角的矩阵的元素的和为例。
先看一张区域分割图:
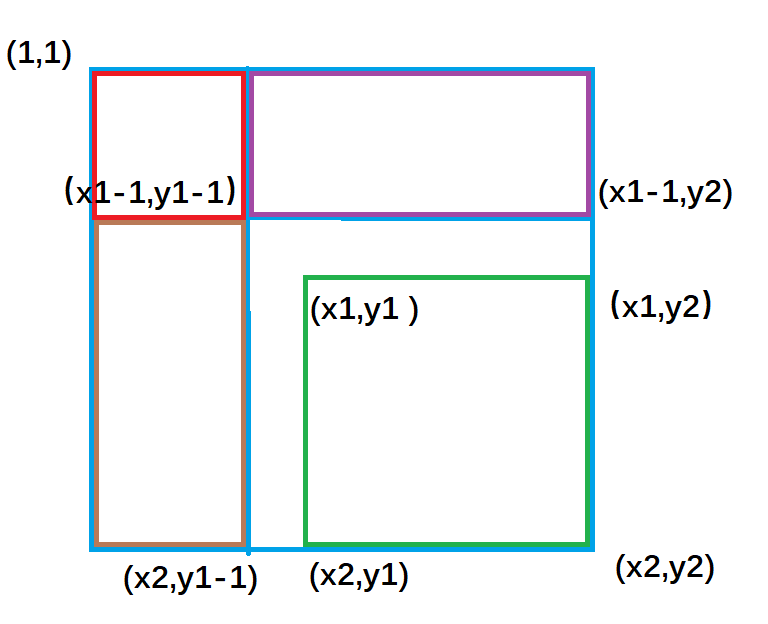
再看具体的计算:
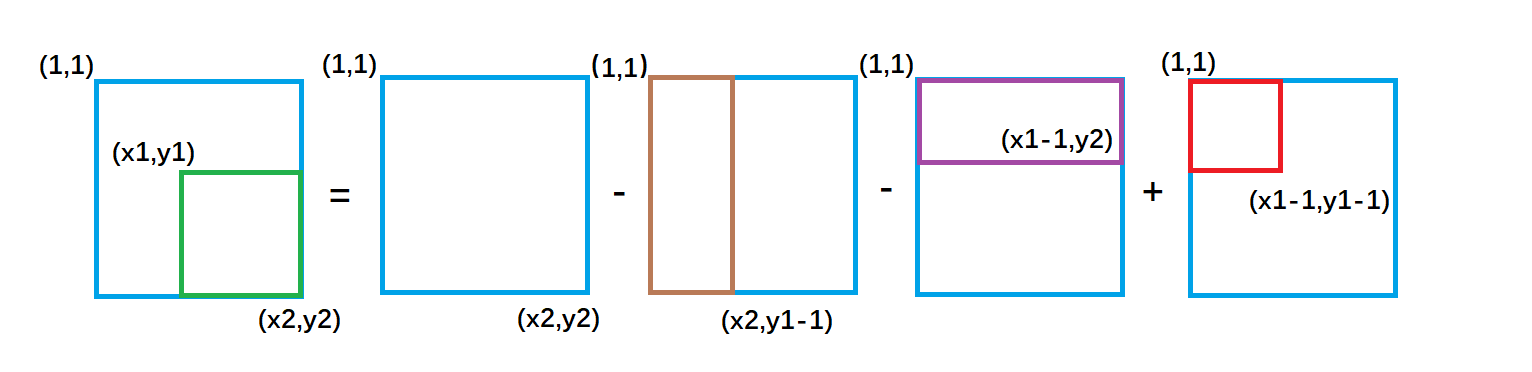
紫色面积是指 ( 1,1 )到(x1-1,y2)的矩形面积 , 棕色面积是指(1,1)到(x2,y1-1)的矩形面积;不难得出:绿色矩形的面积 = 整个外围面积s[x2, y2] - 棕色面积s[x2, y1 - 1] - 紫色面积s[x1 - 1, y2] + 重复减去的红色面积 s[x1 - 1, y1 - 1]。
所以,以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]
这就是二维前缀和。

示例:
1 | |
输出:
1 | |
2.差分

差分可以看成前缀和的逆运算。类似于积分和微分。
2.1 一维差分
差分数组
已知一个原数组a:a[1], a[2], a[3],,,,,, a[n];
然后构造一个数组b : b[1] ,b[2] , b[3],,,,,, b[i];
使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]
也就是说,a数组是b数组的前缀和数组,反过来我们把b数组叫做a数组的差分数组。换句话说,每一个a[i]都是b数组中从头开始的一段区间和。我们只要有b数组,通过前缀和运算,就可以在O(n) 的时间内得到a数组 。
至于考虑如何构造差分b数组。这个我们现在不需要关心,其实也没有必要关心如何构造b数组。往后面看就明白为什么了。
差分原理
首先,需要知道两个数组,一个原数组a,一个差分数组b。
首先明白的是,a数组是b数组的前缀和,b数组是a数组的差分数组。即b数组相当于是原数组,a数组是b数组的前缀和。
明白后,想一个问题。如果b[1]加上1,那么a数组怎么变?是不是a[1]及后面的所有数都会加上1。因为a数组是b数组的前缀和,a[i]存的是b的前i个数的和。
即:差分b数组中的 b[i] + c ,通过前缀和运算后,a数组变成 a[i] + c ,a[i+1] + c,,,,,, a[n] + c;
最好自行在纸上画画。
好。明白上面后。单个修改没问题了。那我们再来算一个区间的。把a数组中的[ l, r]区间中的每一个数都加上c。
最容易想到的就是对b[l]+c,那么a[l]及其后面的数都加上了c。然后对b[r]+c吗?这不是就不对了嘛。
对b[r+1]-c即可,那么a[r+1]及其后面的都减去了c,就把前面加的抵消了。见图。
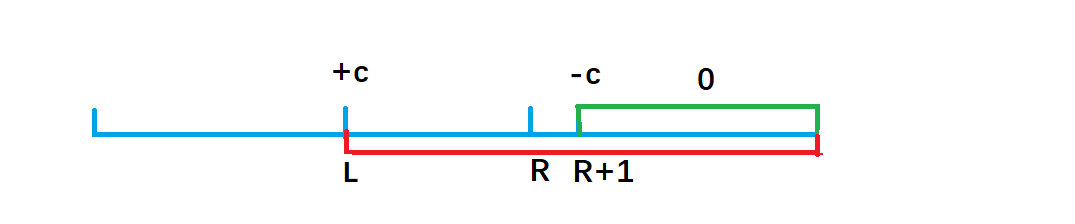
b[l] + c,效果使得a数组中 a[l]及以后的数都加上了c(红色部分),但我们只要求l到r区间加上c, 因此还需要执行 b[r+1] - c,让a数组中a[r+1]及往后的区间再减去c(绿色部分),这样对于a[r] 以后区间的数相当于没有发生改变。
一维差分结论:给a数组中的[ l, r]区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c即可。
这就是一维差分数组。

差分数组的构造
前面说了,这个不需要我们关心的。只需要明白了上面的原理即可。因为,我们只需要把原数组a中的数也当成是要操作的数即可。
即,我们一开始可以把a数组和b数组都当成0,即a、b数组全是0。然后,对于每一个a数组中的数,我们都可以看成是一次修改,进而在b数组中进行操作。例如,a[1]=3,a[2]=10。即,在b数组的区间[1,1]中加上3,b数组的区间[2,2]中加上10。
所以,对于差分数组如何构造,我们无需知道。
示例:
1 | |
输出:
1 | |
当然了,如果非要自己去构造的话也是可以的,这里也提供一种构造方法。
如下:
a[0 ]= 0;
b[1] = a[1] - a[0];
b[2] = a[2] - a[1];
b[3] =a [3] - a[2];
……..
b[n] = a[n] - a[n-1];
如图:

2.2 二维差分
同理在二维中,a[][]数组是b[][]数组的前缀和数组,那么b[][]是a[][]的差分数组。至于差分数组的构造在一维中已经说的很明白了。
问题:已知原数组a中被选中的子矩阵为 以(x1,y1)为左上角,以(x2,y2)为右上角所围成的矩形区域。
始终要记得,a数组是b数组的前缀和数组,比如对b数组的b[i][j]的修改,会影响到a数组中从a[i][j]及往后的每一个数。
原理
先看一张区域分割图:

再来看具体的分割:
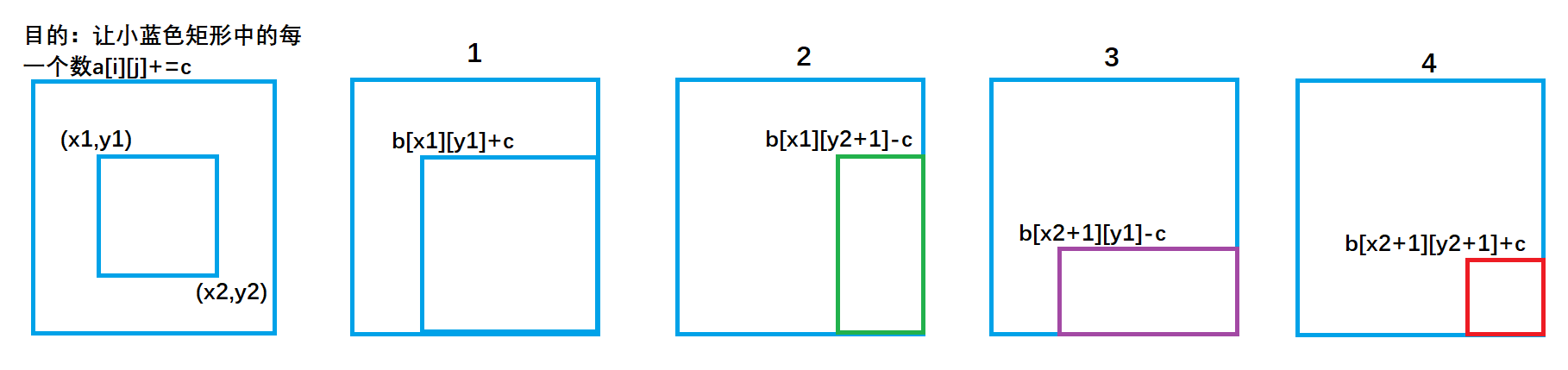
b[x1][ y1 ] +=c ; 对应编号图1 ,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1][y2+1]-=c ; 对应编号图2 ,让整个a数组中绿色矩形面积的元素再减去c,使其a数组内元素不发生改变。
b[x2+1][y1]- =c ; 对应编号图3 ,让整个a数组中紫色矩形面积的元素再减去c,使其a数组内元素不发生改变。
b[x2+1][y2+1]+=c; 对应编号图4,让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再加上一次c,才能使其恢复。
这里,再说一下为什么不用构造差分数组。因为我们可以先假想a数组为空,那么b数组一开始也为空,但是实际上a数组并不为空,因此我们每次让以(i,j)为左上角到以(i,j)为右下角面积内元素(其实就是一个小方格的面积)去插入 c=a[i][j],等价于原数组a中(i,j) 到(i,j)范围内 加上了 a[i][j] ,因此执行n * m次插入操作,就成功构建了差分b数组。
实现:
1 | |
当然了,二维差分操作也有直接的构造方法,公式如下:
b[i][j]=a[i][j]−a[i−1][j]−a[i][j−1]+a[i−1][j−1]
构造同一维差分那里的思维相同。这里不再说了。
这就是二维差分。

3.总结
一句话:前缀和受影响的向前看,差分受影响的向后看。
本文作者: 墨水记忆
本文链接: https://tothefor.com/DragonOne/1936213498.html
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
