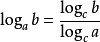本文最后更新于:May 13, 2023 pm
积土成山,风雨兴焉;积水成渊,蛟龙生焉;积善成德,而神明自得,圣心备焉。故不积跬步,无以至千里,不积小流无以成江海。齐骥一跃,不能十步,驽马十驾,功不在舍。面对悬崖峭壁,一百年也看不出一条裂缝来,但用斧凿,能进一寸进一寸,能进一尺进一尺,不断积累,飞跃必来,突破随之。
题目
题目链接
大致题意:求有多少个y能使x^y=z(本博客内容中^均为异或操作),且y<x。其中z为质数(素数)。
📢提示:本题解仅供参考。太菜了,只能写成这样。。。
前知
2.0 数的二进制长度
可以利用对数算出来,使用到log2(N)。但是java中只有log(double)(以e为底的),log10(double)等等函数,这时用换底公式就可以自己实现log2(N)。C++中有log2(x)的函数。
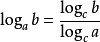
log2N=logeN/loge2,logeN代表以e为底的N的对数,loge2代表以e为底的2的对数。
Java中还有一种简单的方法:
| System.out.println(Integer.toBinaryString(2).length());
System.out.println(Integer.toBinaryString(3).length());
System.out.println(Integer.toBinaryString(5).length());
System.out.println(Integer.toBinaryString(7).length());
System.out.println(Integer.toBinaryString(11).length());
System.out.println((int) (Math.log(2)/Math.log(2)));
System.out.println((int) (Math.log(3)/Math.log(2)));
System.out.println((int) (Math.log(5)/Math.log(2)));
System.out.println((int) (Math.log(7)/Math.log(2)));
System.out.println((int) (Math.log(11)/Math.log(2)));
|
📢注意:上面两种方式算出来的结果不一样,相差1。用第一种求数组二进制位长度要减1,用第二种求数的二进制位不需要减1,至于为什么,我也不知道,等后面的官方题解吧。也许是因为如果是小数代表他们还没到更高位 那就还是第i位。
2.1 题意转换
因为x^y=z,所以y=x^z。所以,可以通过素数和给定的x来求y。
📢提示:可以直接先看过程演示。
2.2 二进制(重点)
我们需要知道一个数的二进制位中的最高位(最右边)的1处于第几位。例如:
3 -> 11,则为2位。(10)
7 -> 111,则为3位。(100)
11 -> 1011,则为4位。(1000)
这个是用在素数上的。如果一个素数T的二进制为1010101,那么最后我们需要的只是他的最高位的1所处的位置,这个素数我们处理后为:1000000。
这样处理的好处是:1000000到1111111之间的所有素数都可以这样表示。而当我们求一个比1000000大的素数时,直接加上这样长度的素数有多少个即可(所以,可以用一个数组cnt[i]来表示以1开始的,长度为i的,素数的二进制数的个数)。当然了,这样算出来的只是表示了1000000到1111111之间的所有素数;我们还需要求100000到111111之间的所有素数、10000到11111之间的所有素数、….、10到11之间的所有素数、1到1之间的所有素数。
但在本题中,是找小于x的y。而y=x^z,所以,
2.3 素数范围
题目给出的x的范围为1 * 106。又因为y=x^z。所以素数可能会存在于x范围外,所以找素数时需要找更大的范围。多找一倍即可。
2.4 原理(补充)
我们需要先知道:
1000 ^ 1xxx 的结果一定小于 1000。
再如:10010 ^ 1xxxx 的结果一定小于 10010。
而题目要求在转换后,变为了y=x^z。其中x已知,z为素数(可以自行求)。
假如x的二进制为:1,则我们进行操作:1 ^ 1 。结果一定小于x。
假如x的二进制位:11,则进行操作:11 ^ 10 。结果一定小于x。
假如x的二进制位:111,则进行操作:111 ^ 100 。结果一定小于x。
假如x的二进制位:1111,则进行操作:1111 ^ 1000 。结果一定小于x。
….
但,这样一次我们只是找到了最高位的1的那一部分。在2.2中也说到了。
过程演示
示例1:x=10。
- 我们先求出素数。用cnt[i]表示:有多少个素数的二进制数的长度为i。
素数有:2、3、5、7、11、13、17、19、23、…. 。
二进制分别为:(1不是素数,所以cnt[1]=0)
2:10 -> 10 cnt[2]
3:11 -> 10 cnt[2]
5:101 -> 100 cnt[3]
7:111 -> 100 cnt[3]
11:1011 -> 1000 cnt[4]
13:1101 -> 1000 cnt[4]
17:10001 -> 10000 cnt[5]
19:10011 -> 10000 cnt[5]
23:10111 -> 10000 cnt[5]
….
- 再将x=10转化为二进制:1010
然后我们从右向左(低位到高位)进行计算:(我们只计算二进制位是1的)
第二位是1,我们的最后结果ans+=cnt[2];
第四位是1,我们的最后结果ans+=cnt[4];
最后结果:4
示例2:x=9
第一步同理示例1,求出所有素数。
再将x=9转化为二进制:1001
这里是第一位和第四位为1,所以ans分别加上cnt[1]和cnt[4]即可,最后结果为2。
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| import java.io.*;
import java.util.*;
public class Main {
public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));
public static Scanner sc = new Scanner(System.in);
public static int[] cnt = new int[2000000];
public static void main(String[] args) throws Exception {
for(int i=2;i<=1500000;++i){
if(isPrime_3(i)){
cnt[Integer.toBinaryString(i).length()-1]++;
}
}
int t = nextInt();
while(t--!=0){
int ans = 0;
int ma = nextInt();
for(int i=0;i<=20;++i){
if(((ma>>i)&1)==1){
ans+=cnt[i];
}
}
cout.println(ans);
cout.flush();
}
closeAll();
}
public static boolean isPrime_3( int num )
{
if(num ==2|| num==3 )
return true ;
if(num %6!= 1&&num %6!= 5)
return false;
int tmp = (int) Math.sqrt( num);
for(int i= 5;i <=tmp; i+=6 )
if(num %i== 0||num %(i+ 2)==0 )
return false ;
return true ;
}
public static int nextInt() throws Exception {
cin.nextToken();
return (int) cin.nval;
}
public static long nextLong() throws Exception {
cin.nextToken();
return (long) cin.nval;
}
public static double nextDouble() throws Exception {
cin.nextToken();
return cin.nval;
}
public static String nextString() throws Exception {
cin.nextToken();
return cin.sval;
}
public static void closeAll() throws Exception {
cout.close();
in.close();
out.close();
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| import java.io.*;
import java.util.*;
public class Main {
public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));
public static Scanner sc = new Scanner(System.in);
public static int[] cnt = new int[2000000];
public static void main(String[] args) throws Exception {
for(int i=2;i<=1500000;++i){
if(isPrime_3(i)){
cnt[(int) (Math.log(i)/Math.log(2))]++;
}
}
int t = nextInt();
while(t--!=0){
int ans = 0;
int ma = nextInt();
for(int i=0;i<=20;++i){
if(((ma>>i)&1)==1){
ans+=cnt[i];
}
}
cout.println(ans);
cout.flush();
}
closeAll();
}
public static boolean isPrime_3( int num )
{
if(num ==2|| num==3 )
return true ;
if(num %6!= 1&&num %6!= 5)
return false;
int tmp = (int) Math.sqrt( num);
for(int i= 5;i <=tmp; i+=6 )
if(num %i== 0||num %(i+ 2)==0 )
return false ;
return true ;
}
public static int nextInt() throws Exception {
cin.nextToken();
return (int) cin.nval;
}
public static long nextLong() throws Exception {
cin.nextToken();
return (long) cin.nval;
}
public static double nextDouble() throws Exception {
cin.nextToken();
return cin.nval;
}
public static String nextString() throws Exception {
cin.nextToken();
return cin.sval;
}
public static void closeAll() throws Exception {
cout.close();
in.close();
out.close();
}
}
|