算法学习-并查集模板（JAVA实现）

本文最后更新于：April 4, 2022 pm

纸上得来终觉浅，绝知此事要躬行。路漫漫其修远兮，吾将上下而求索！知识是经过历史的巨人沉淀下来的，别总想着自己能够快速学会，多花点时间去看看，也许会发现些不同的东西。你能快速学会的、觉得简单的东西，对于别人来说也是一样的。人外有人，天外有天。当努力到达了一定的程度，幸运自会与你不期而遇。

目录

碰到了一个感觉可以用并查集解决的题，所以就复习一下普通并查集吧。因为学过也比较熟悉，所以本文主要是记录一下模板。

题目链接（大致思路：从1开始，把经过的点都合并起来，最后看要求的点的根节点是否是1即可。AC代码见最后。）

并查集（Union-find Sets）是一种非常精巧而实用的数据结构，它主要用于处理一些不相交集合的合并问题。一些常见的用途有求连通子图、求最小生成树的 Kruskal 算法和求最近公共祖先（Least Common Ancestors, LCA）等。

它用于处理一些不交集的 合并 及 查询 问题。 它支持两种操作：

  • 查找（Find）：确定某个元素处于哪个子集；
  • 合并（Union）：将两个子集合并成一个集合。

在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合（即自己单独一个集合），然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。

普通并查集模板

并查集(带路径压缩)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//并查集(路径压缩)

//par数组用来存储根节点，par[x]=y表示x的根节点为y
static int[] par = new int[10005];
//初始化
public static void init(int n){
    for (int i = 1; i <= n; i++) {
        par[i]=i;
    }
}
//查找x所在集合的根
public static int find(int x){
    if(par[x]!=x) par[x]=find(par[x]); //递归返回的同时压缩路径
    return par[x];
}
//合并x与y所在集合
public static void unite(int x,int y){
    int tx = find(x);
    int ty = find(y);
    if(tx!=ty){ //不是同一个根，即不在同一个集合，就合并
        par[tx]=ty;
    }
}

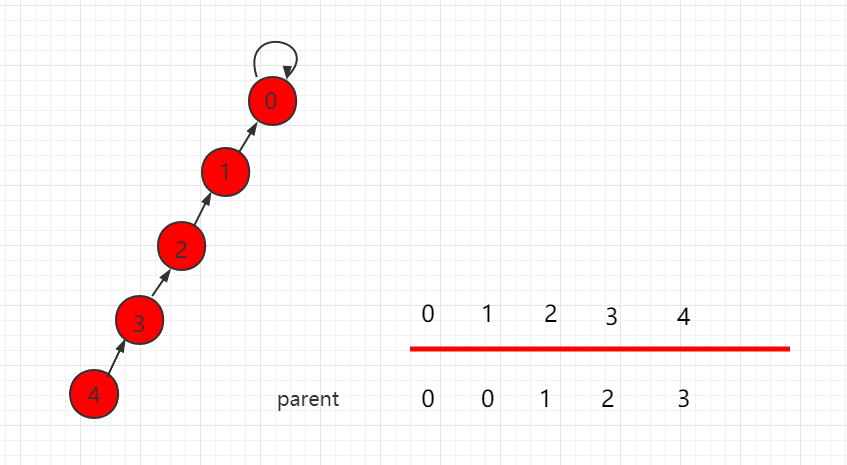
路径压缩理解：

从开始的这样

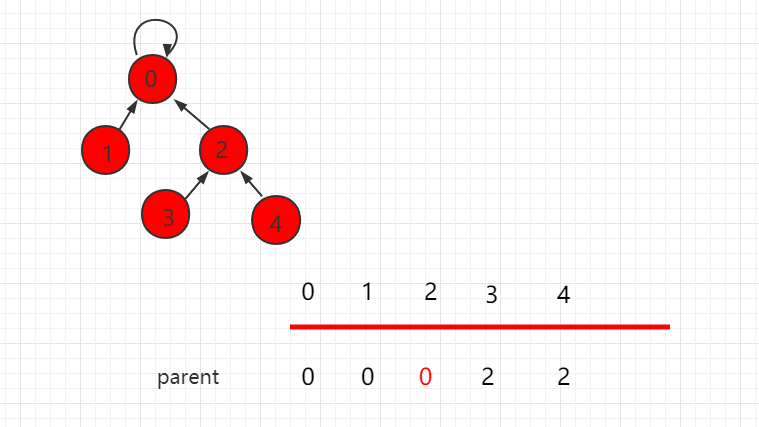
变成这样

再变成这样

最后变成了这样

维护集合中元素的个数

用来计算每一个集合中元素的个数有多少。在普通并查集的基础上加一个数组来统计每一个集合中元素的个数即可。在初始化的时候每一个集合中的个数都为1，在合并的时候将子节点中的元素个数加到根节点的元素个数中去。

就只是在普通并查集的基础上修改两个地方：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//初始化
public static void init(int n){
    for (int i = 1; i <= n; i++) {
        par[i]=i;
        sum[i]=1; //每一个集合开始都是1
    }
}

//合并x与y所在集合
public static void unite(int x,int y){
    int tx = find(x);
    int ty = find(y);
    if(tx!=ty){
        par[tx]=ty; //让ty成为tx的根节点
        sum[ty]+=sum[tx]; //让根节点加上子节点中的元素个数
    }
}

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//并查集(路径压缩)
static int[] par = new int[10005];
//sum数组用来存储每一个集合中的元素个数
static int[] sum = new int[10005];
//初始化
public static void init(int n){
    for (int i = 1; i <= n; i++) {
        par[i]=i;
        sum[i]=1;
    }
}
//查找x所在集合的根
public static int find(int x){
    if(par[x]!=x) par[x]=find(par[x]); //递归返回的同时压缩路径
    return par[x];
}
//合并x与y所在集合
public static void unite(int x,int y){
    int tx = find(x);
    int ty = find(y);
    if(tx!=ty){
        par[tx]=ty;
        sum[ty]+=sum[tx];
    }
}

维护节点到根节点的距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
import java.io.*;
import java.text.SimpleDateFormat;
import java.util.*;

/**
 * @Author DragonOne
 * @Date 2021/12/5 21:27
 * @墨水记忆 www.tothefor.com
 */

public class Main {
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));
    public static Scanner sc = new Scanner(System.in);
    /**
     * 每月的天数
     */
    public static int monthes[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
    public static int maxd = 200000000 + 15;
    public static int INF = 0x3f3f3f3f;
    public static int mod = (int) 1e9 + 7;
    public static int[][] fx = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
    public static int[] par = new int[maxd]; //par[i]表示i的父节点
    public static int[] dis = new int[maxd]; //dis[i]表示i到根节点的距离

    public static int find(int x){
        if(par[x]!=x){
            int t = par[x];
            par[x]=find(par[x]);
            dis[x]+=dis[t]; //x到根节点的距离 就等于 x到父节点的距离 加上 x的父节点到根节点的距离。之所以有x到父节点的距离，是因为在最开始添加关系的时候，我们默认添加的是x到父节点的关系。
//            return par[x];
        }
        return par[x];
    }

    public static void main(String[] args) throws Exception {

        int n = nextInt();
        for(int i=1;i<=n;++i) par[i] = i;
        for(int i=1;i<=n-1;++i){
            int x = nextInt();
            int y = nextInt();
            par[y]=x; //x是y的父节点
            dis[y]=1; //当y最开始赋父节点时，默认此时的父节点就是他的根节点，就更新到根节点的距离为1，然后当需要查询他到根节点的距离时，在查询方法中就会更新至到真正根节点的距离。
        }
        for(int i=1;i<=n;++i) {
            int p = find(i);
            System.out.println(i+" 到 "+p+" 的距离为："+dis[i]);
        }
/**
 * 5
 * 1 2
 * 1 5
 * 2 3
 * 2 4
 *
 * 输出
 * 1 到 1 的距离为：0
 * 2 到 1 的距离为：1
 * 3 到 1 的距离为：2
 * 4 到 1 的距离为：2
 * 5 到 1 的距离为：1
 */

        closeAll();
    }

    public static int gcd(int a, int b) { // 不需要判断a和b的大小
        while (b > 0) {
            a %= b;
            b ^= a;
            a ^= b;
            b ^= a;
        }
        return a;
    }

    public static int log(int x) { //log方法是以2为底,求x的对数.而java自带的log是以e为底的
        return (int) (Math.log(x) / Math.log(2));
    }

    public static void cinInit() {
        cin.wordChars('a', 'z');
        cin.wordChars('A', 'Z');
        cin.wordChars(128 + 32, 255);
        cin.whitespaceChars(0, ' ');
        cin.commentChar('/');
        cin.quoteChar('"');
        cin.quoteChar('\'');
        cin.parseNumbers(); //可单独使用还原数字
    }

    public static int nextInt() throws Exception {
        cin.nextToken();
        return (int) cin.nval;
    }

    public static long nextLong() throws Exception {
        cin.nextToken();
        return (long) cin.nval;
    }

    public static double nextDouble() throws Exception {
        cin.nextToken();
        return cin.nval;
    }

    public static String nextString() throws Exception {
        cin.nextToken();
        return cin.sval;
    }

    public static void closeAll() throws Exception {
        cout.close();
        in.close();
        out.close();
    }
}

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
import javafx.util.Pair;

import java.io.*;
import java.text.DecimalFormat;
import java.util.*;

/**
 * @Author DragonOne
 * @Date 2021/12/5 21:27
 * @墨水记忆 www.tothefor.com
 */
public class Main {
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));

    public static int[] par = new int[100005];

    public static void main(String[] args) throws Exception {
        cin.nextToken();
        int n = (int) cin.nval;
        init(n);
        cin.nextToken();
        int t = (int) cin.nval;
        int[] f = new int[n + 5];
        for (int i = 1; i <= n - 1; ++i) {
            cin.nextToken();
            f[i] = (int) cin.nval;
        }
        for(int i=1;i<n;){
            int sm = i + f[i];
            if(sm<=n){
                unite(i,sm);
            }
            i = i + f[i];
        }
        if(par[t]==1){
            cout.println("YES");
            cout.flush();
        }else{
            cout.println("NO");
            cout.flush();
        }

        closeAll();
    }

    public static void init(int x) {
        for (int i = 1; i <= x; ++i) {
            par[i] = i;
        }
    }

    public static int find(int x) {
        if (par[x] != x) par[x] = find(par[x]);
        return par[x];
    }

    public static void unite(int x, int y) { //注意顺序，谁是谁的根节点
        int tx = find(x);
        int ty = find(y);
        if (tx != ty) {
            par[ty] = tx;
        }
    }

    public static void closeAll() throws Exception {
        cout.close();
        in.close();
        out.close();
    }

}