算法学习-二分图的判断及其最大匹配模板（JAVA实现）

本文最后更新于：May 13, 2023 pm

纸上得来终觉浅，绝知此事要躬行。路漫漫其修远兮，吾将上下而求索！知识是经过历史的巨人沉淀下来的，别总想着自己能够快速学会，多花点时间去看看，也许会发现些不同的东西。你能快速学会的、觉得简单的东西，对于别人来说也是一样的。人外有人，天外有天。当努力到达了一定的程度，幸运自会与你不期而遇。

目录

提示：若无特殊说明，n表示点的个数，m表示边的条数。

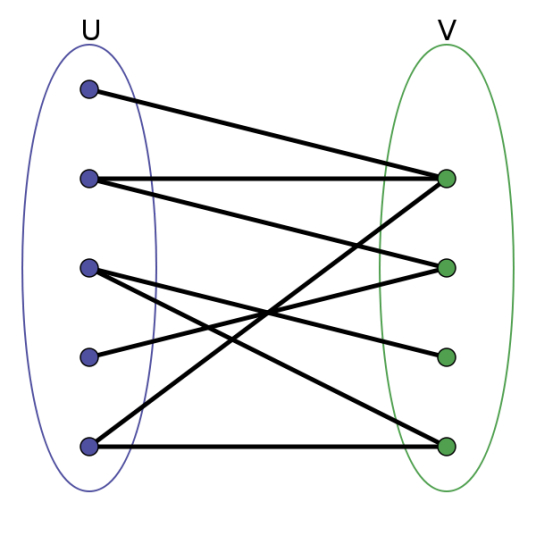
预知

二分图：简而言之，就是顶点集可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻(相连)。如图：

奇数环：一个环中的点的个数是奇数（或边的长度为偶数）。如下图：

性质：二分图当且仅当图中不含有奇数环。（二分图判断条件）

染色法

时间复杂度：O(n+m)。

常用于判断一个图是不是二分图。

题意:

给定一个含有n个点m条边的无向图，图中可能存在重边和自环。现在判断此图是否是二分图。

输入两个整数n和m。

接下来m行分别两个整数u和v，表示u点到v点之间存在一条边。

是二分图输出”YES”，否则输出”NO”。

1≤n，m≤105

测试数据

输入：

1
2
3
4
5
4 4
1 3
1 4
2 3
2 4

输出：

1
YES

DFS实现

用 1 和 2 区分不同颜色，0 表示未染色。

遍历所有点（因为没有说明是连通图），对未染色点进行染色（dfs）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
import java.io.*;
import java.math.BigInteger;
import java.util.*;


/**
 * @Author DragonOne
 * @Date 2021/12/5 21:27
 * @墨水记忆 www.tothefor.com
 */
public class Main {
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));
    public static Scanner sc = new Scanner(System.in);

    public static int maxd = 2000+7;
    public static int INF = 0x3f3f3f3f;
    public static int mod = 998244353;

    public static int[] head = new int[maxd];
    public static int[] edgePre = new int[maxd];
    public static int[] edgeTo = new int[maxd];
    public static int[] color = new int[maxd]; //编号0表示未染色，编号1表示染色为一类，编号2表示另一类
    public static int node = 0;

    public static void init(int n,int m){
        for(int i=1;i<=n;++i){
            head[i]=-1;
            color[i]=0;
        }
        node=0;
    }
    public static void add_edge(int a,int b){
        edgeTo[node]=b;
        edgePre[node]=head[a];
        head[a]=node++;
    }
    public static boolean dfs(int u,int c){ //true为二分图，false为非二分图
        color[u] = c;
        for(int i=head[u];i!=-1;i=edgePre[i]){ //染色与当前点有边的点，并将其染色为与此点相反的一种颜色
            int v = edgeTo[i];
            if(color[v]==0){ //若没有被染色，则进行染不同颜色
                if(!dfs(v,3-c)){ //3-c表示染和c不同的颜色，因为这里只有1、2两种颜色，所以用3减当前颜色就是相反的颜色
                    return false; //染色失败
                }
            }else if(color[v]==c){ //如果已经染色了，但和前一个点是相同的颜色
                return false;
            }
        }
        return true;
    }

    public static void main(String[] args) throws Exception {

        int n = nextInt();
        int m = nextInt();
        init(n,m);
        while(m-->0){
            int a = nextInt();
            int b = nextInt();
            add_edge(a,b); //无向图
            add_edge(b,a);
        }
        boolean flag = true; //用来标记最后的结果是否是二分图，默认是二分图
        for(int i=1;i<=n;++i){//遍历所有点是为了防止图不连通，若是连通图，则不需要遍历所有点
            if(color[i]==0){ //没有被染色
                if(!dfs(i,1)){ //若不是二分图。这里初始染色为1，也可以染色为2，自定义
                    flag=false;
                    break;
                }
            }
        }
        if(flag) System.out.println("YES"); //是二分图
        else System.out.println("NO");

        closeAll();
    }

    public static void cinInit(){
        cin.wordChars('a', 'z');
        cin.wordChars('A', 'Z');
        cin.wordChars(128 + 32, 255);
        cin.whitespaceChars(0, ' ');
        cin.commentChar('/');
        cin.quoteChar('"');
        cin.quoteChar('\'');
        cin.parseNumbers(); //可单独使用来还原数字
    }

    public static int nextInt() throws Exception{
        cin.nextToken();
        return (int) cin.nval;
    }
    public static long nextLong() throws Exception{
        cin.nextToken();
        return (long) cin.nval;
    }
    public static double nextDouble() throws Exception{
        cin.nextToken();
        return cin.nval;
    }
    public static String nextString() throws Exception{
        cin.nextToken();
        return cin.sval;
    }
    public static void closeAll() throws Exception {
        cout.close();
        in.close();
        out.close();
    }

}

BFS实现

  • 颜色 1 和 2 表示不同颜色， 0 表示 未染色。遍历所有点（因为没有说明是连通图），对未染色点进行染色（bfs）。

  • 队列中存储<点编号, 颜色>。

具体思路：

  1. 队列初始化，将第 i 个点入队, 默认颜色可以是 1 或 2。
  1. 当队列不为空时（while()），每次获取队列首元素，并遍历与首元素有边的点。

  1. 若邻边的点未染色则染上与 首元素相反的颜色，并添加到队列。

    若邻边的点已经染色且与首元素的颜色相同，则返回 false。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
import java.io.*;
import java.math.BigInteger;
import java.util.*;


/**
 * @Author DragonOne
 * @Date 2021/12/5 21:27
 * @墨水记忆 www.tothefor.com
 */
public class Main {
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));
    public static Scanner sc = new Scanner(System.in);

    public static int maxd = 2000+7;
    public static int INF = 0x3f3f3f3f;
    public static int mod = 998244353;

    public static int[] head = new int[maxd];
    public static int[] edgePre = new int[maxd];
    public static int[] edgeTo = new int[maxd];
    public static int[] color = new int[maxd]; //0表示未染色，编号1表示染色为一类，编号2表示另一类
    public static int node = 0;

    public static class POT{
        private int point; //点编号
        private int color; //颜色编号

        public POT() {
        }
        public POT(int point, int color) {
            this.point = point;
            this.color = color;
        }
    }

    public static void init(int n,int m){
        for(int i=1;i<=n;++i){
            head[i]=-1;
            color[i]=0;
        }
        node=0;
    }
    public static void add_edge(int a,int b){
        edgeTo[node]=b;
        edgePre[node]=head[a];
        head[a]=node++;
    }
    public static boolean bfs(int u,int c){ //true为二分图，false为非二分图
        Queue<POT> q = new ArrayDeque<>();
        q.add(new POT(u,c)); //将点入队
        color[u]=c; //染色为c
        while(!q.isEmpty()){
            POT mid = q.poll();
            int v = mid.point;
            int cc = mid.color;
            for(int i=head[v];i!=-1;i=edgePre[i]){ //遍历与当前点有边的点
                int vv = edgeTo[i];
                if(color[vv]==0){ //如果未被染色
                    color[vv]=3-cc;
                    q.add(new POT(vv,3-cc));
                }else if(color[vv]==cc){ //如果已经染色了，但和前一个点的染色情况一样
                    return false;
                }
            }
        }
        return true;
    }

    public static void main(String[] args) throws Exception {

        int n = nextInt();
        int m = nextInt();
        init(n,m);
        while(m-->0){
            int a = nextInt();
            int b = nextInt();
            add_edge(a,b); //无向图
            add_edge(b,a);
        }
        boolean flag = true; //用来标记最后的结果是否是二分图，默认是二分图
        for(int i=1;i<=n;++i){ //遍历所有点是为了防止图不连通，若是连通图，则不需要遍历所有点
            if(color[i]==0){ //没有被染色
                if(!bfs(i,1)){ //若不是二分图
                    flag=false;
                    break;
                }
            }
        }
        if(flag) System.out.println("YES"); //是二分图
        else System.out.println("NO");

        closeAll();
    }

    public static void cinInit(){
        cin.wordChars('a', 'z');
        cin.wordChars('A', 'Z');
        cin.wordChars(128 + 32, 255);
        cin.whitespaceChars(0, ' ');
        cin.commentChar('/');
        cin.quoteChar('"');
        cin.quoteChar('\'');
        cin.parseNumbers(); //可单独使用来还原数字
    }

    public static int nextInt() throws Exception{
        cin.nextToken();
        return (int) cin.nval;
    }
    public static long nextLong() throws Exception{
        cin.nextToken();
        return (long) cin.nval;
    }
    public static double nextDouble() throws Exception{
        cin.nextToken();
        return cin.nval;
    }
    public static String nextString() throws Exception{
        cin.nextToken();
        return cin.sval;
    }
    public static void closeAll() throws Exception {
        cout.close();
        in.close();
        out.close();
    }

}

并查集判断二分图

我们知道如果是二分图的话，那么图中每个顶点的所有邻接点都应该属于同一集合，且不与顶点处于同一集合。因此我们可以使用并查集来解决这个问题，我们遍历图中每个顶点，将当前顶点的所有邻接点进行合并，并判断这些邻接点中是否存在某一邻接点已经和当前顶点处于同一个集合中了，若是，则说明不是二分图。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
import java.io.*;
import java.math.BigInteger;
import java.util.*;


/**
 * @Author DragonOne
 * @Date 2021/12/5 21:27
 * @墨水记忆 www.tothefor.com
 */
public class Main {
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));
    public static Scanner sc = new Scanner(System.in);

    public static int maxd = 2000+7;
    public static int INF = 0x3f3f3f3f;
    public static int mod = 998244353;

    public static int[] head = new int[maxd];
    public static int[] edgePre = new int[maxd];
    public static int[] edgeTo = new int[maxd];
    public static int[] par = new int[maxd];
    public static int node = 0;

    public static int find(int x){
        if(x!=par[x]) par[x] = find(par[x]);
        return par[x];
    }
    public static void unite(int a,int b){
        int x = find(a);
        int y = find(b);
        if(x!=y){
            par[x]=y;
        }
    }

    public static void init(int n,int m){
        for(int i=1;i<=n;++i){
            head[i]=-1;
            par[i]=i;
        }
        node=0;
    }
    public static void add_edge(int a,int b){
        edgeTo[node]=b;
        edgePre[node]=head[a];
        head[a]=node++;
    }
    public static boolean bjc(int n){ //true为二分图，false为非二分图
        for(int i=1;i<=n;++i){
            int firstP = edgeTo[head[i]]; //得到当前点i的第一个邻接点
            for(int j=head[i];j!=-1;j=edgePre[j]){ //遍历当前点i的所有邻接点
                int v = edgeTo[j];
                if(find(i)==find(v)){ //如果i的邻接点与i在同一集合中
                    return false;
                }
                unite(firstP,v); //如果i的邻接点与i不在同一集合中，则将i的邻接点与邻接点进行合并
            }
        }
        return true;

    }

    public static void main(String[] args) throws Exception {

        int n = nextInt();
        int m = nextInt();
        init(n,m);
        while(m-->0){
            int a = nextInt();
            int b = nextInt();
            add_edge(a,b); //无向图
            add_edge(b,a);
        }

        if(bjc(n)) System.out.println("YES"); //是二分图
        else System.out.println("NO");

        closeAll();
    }

    public static void cinInit(){
        cin.wordChars('a', 'z');
        cin.wordChars('A', 'Z');
        cin.wordChars(128 + 32, 255);
        cin.whitespaceChars(0, ' ');
        cin.commentChar('/');
        cin.quoteChar('"');
        cin.quoteChar('\'');
        cin.parseNumbers(); //可单独使用来还原数字
    }

    public static int nextInt() throws Exception{
        cin.nextToken();
        return (int) cin.nval;
    }
    public static long nextLong() throws Exception{
        cin.nextToken();
        return (long) cin.nval;
    }
    public static double nextDouble() throws Exception{
        cin.nextToken();
        return cin.nval;
    }
    public static String nextString() throws Exception{
        cin.nextToken();
        return cin.sval;
    }
    public static void closeAll() throws Exception {
        cout.close();
        in.close();
        out.close();
    }

}

匈牙利算法

时间复杂度：O(n*m)，实际运行时间一般远小于O(n*m)。

常用于给定一个二分图，求最大匹配。

最大匹配：两个集合看成两个性别（男、女），点看出人（男生、女生）。最大匹配就是能凑出多少对情侣，前提是两个人互相认识（相连）。

题意：

  • 枚举男生点集，那么边的存储就只是从男生指向女生。因为只会找男生对应的所有女生，而不会寻找女生对应的所有男生。（从女生点集开始也可以，其他的反着来即可。）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
import java.io.*;
import java.math.BigInteger;
import java.util.*;


/**
 * @Author DragonOne
 * @Date 2021/12/5 21:27
 * @墨水记忆 www.tothefor.com
 */
public class Main {
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));
    public static Scanner sc = new Scanner(System.in);

    public static int maxd = 2000+7;
    public static int INF = 0x3f3f3f3f;
    public static int mod = 998244353;

    public static int[] head = new int[maxd];
    public static int[] edgePre = new int[maxd];
    public static int[] edgeTo = new int[maxd];
    public static int node = 0;
    public static int[] match = new int[maxd]; //用来存储妹子的男友是谁
    public static boolean[] vis = new boolean[maxd]; //对于某一个男生，用来保存女生是否被男生选中过，保证女生在一个男生的一生中只出现一次

    public static void init(int n){
        for(int i=1;i<=n;++i){
            head[i]=-1;
        }
        node=0;
    }
    public static void add_edge(int a,int b){
        edgeTo[node]=b;
        edgePre[node]=head[a];
        head[a]=node++;
    }
    public static boolean find(int x){ //能否帮x找到女友
        for(int i=head[x];i!=-1;i=edgePre[i]){
            int v = edgeTo[i];
            if(!vis[v]){ //如果之前没有和这个妹子在一起过，那就试一试。否则就是前女友，不要
                vis[v]=true; //之前没有，那就现在试试（但可能现在人家有男友）
                if(match[v]==0||find(match[v])){ //如果没有男友，那就可以；有男友的话，那就看能不能帮她男友再找一个
                    match[v] = x; //没有男友或者成功帮她男友找了另一个，那么你就是她现在的男友
                    return true;
                }
            }
        }
        return false; //尝试了各种办法都找不到女友
    }

    public static void main(String[] args) throws Exception {

        int n1 = nextInt(); //左边集合（男生数量）
        int n2 = nextInt(); //右边集合（女生数量）
        int m = nextInt(); //边数（关系数）
        init(n1);
        while(m-->0){
            int a = nextInt();
            int b = nextInt();
            add_edge(a,b); //自从左指向右（男选女）即可，不用右指左（女选男）
        }

        int ans = 0;
        for(int i=1;i<=n1;++i){ //给所有男生找女友
            Arrays.fill(vis,false); //当前男生和其他所有女生都从没有过 开始
            if(find(i)) ans++;
        }
        System.out.println(ans);
        closeAll();
    }

    public static void cinInit(){
        cin.wordChars('a', 'z');
        cin.wordChars('A', 'Z');
        cin.wordChars(128 + 32, 255);
        cin.whitespaceChars(0, ' ');
        cin.commentChar('/');
        cin.quoteChar('"');
        cin.quoteChar('\'');
        cin.parseNumbers(); //可单独使用来还原数字
    }

    public static int nextInt() throws Exception{
        cin.nextToken();
        return (int) cin.nval;
    }
    public static long nextLong() throws Exception{
        cin.nextToken();
        return (long) cin.nval;
    }
    public static double nextDouble() throws Exception{
        cin.nextToken();
        return cin.nval;
    }
    public static String nextString() throws Exception{
        cin.nextToken();
        return cin.sval;
    }
    public static void closeAll() throws Exception {
        cout.close();
        in.close();
        out.close();
    }

}

最大匹配-自己的一种思路

提示：未验证正确性，只是自己的一种想法。利用贪心思想。每次找对方与异性关系最少的。

  • int man[999]; man[i]表示编号为i的男生与女生的关系的数量。

  • int woman[999]; woman[i]表示编号为i的女生与男生的关系的数量。

  • bool vis[999]; vis[i]表示编号为i的女生已经匹配。

先用男生与女生的关系数量排序（升序），再从某一个性别集合中的人开始（男、女都行），这里以从男生集合中开始。思路就是，从男一号开始，在男一号认识的女生中找到一个特殊的女生，这个特殊的女生满足：认识的男生是最少的并且没有与其他男生配对成功。

然后依次是男二号、男三号。