算法学习-RMQ问题详解及其模板（JAVA实现）

本文最后更新于：March 19, 2022 pm

纸上得来终觉浅，绝知此事要躬行。路漫漫其修远兮，吾将上下而求索！知识是经过历史的巨人沉淀下来的，别总想着自己能够快速学会，多花点时间去看看，也许会发现些不同的东西。你能快速学会的、觉得简单的东西，对于别人来说也是一样的。人外有人，天外有天。当努力到达了一定的程度，幸运自会与你不期而遇。

目录

RMQ问题，即求区间最大（小）值问题。

但有一个条件是：给定的数组是已经不再变化的。

ST算法

ST算法（Sparse Table，稀疏表）主要用于解决区间最值问题（即RMQ问题）。因为ST算法求解RMQ问题时的时间复杂度只有O(n*logn)，查询时间复杂度为常数阶O(1)。虽然还可以使用线段树、树状数组、splay等算法求解区间最值问题，但是ST算法比它们更快，更适用于在线查询。

思路

ST算法分成两部分：离线预处理O(n*logn)和在线查询O(1)。

预处理思路

运用DP思想求解区间最值，并将结果保存到一个二维数组中。不过区间在增加时，每次并不是增加一个长度，而是使用倍增的思想，每次增加2i个长度。

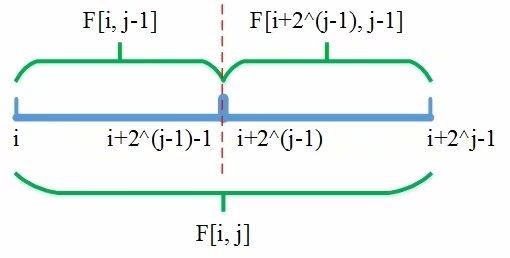
我们定义一个二维数组F[i][j]表示以 i 为起点，区间长度为 2j 的区间的最大（最小）值。此时对应的区间为 [i，i+2j-1]，因为区间长度为 2j 。所以，F[i][0] 表示以 i 为起点，区间长度为1的区间的最大（最下）值，所以，F[i][0] 就等于a[i]，因为区间中就只有一个元素。（a数组表示原数组。）

例如（以找区间最小值为例）：给一个数组a[]={5，4，6，10，1，12}，则 F[0][2] 表示区间以a[0]开始区间长度为 22 的区间：a[0] ~ a[3]；所以 F[0][2] 的最小值为 4。F[2][2] 表示区间[2 ~ 5]的最小值，等于1。

预处理的方法类似于二分，即，将一个区间分为两个小区间，再分别求两个小区间的最值，再求两个小区间最值中的最值。

例如：在求解 F[i][j] 时，ST算法先将长度为 2j 的区间【i，i+2j-1】分成【i，i+2j-1-1】和【i+2j-1 ，i+2j-1+2j-1 -1】两等份，分别对应于 F[i][j-1] 和F[i+2j-1][j-1]（分别是大区间的前半部分和后半部分）。因为区间中元素的个数为 2j 个，所以，从中间平均分成两部分后，每一部分的个数都是 2j-1 个。如图：

然后再求出 区间【i，j-1】 和 【i+2j-1，j-1】的最值，再结合这两个区间的最值求出整个区间的最值。

例如（以找区间最小值为例）：给一个数组a[]={5，4，6，10，1，12}，要求F[1][2]的值，即求区间 【1，4】={4，6，10，1}的最小值。此时，先把区间分为两个小区间【1，2】（对应F[1][1]）和【3，4】（对应F[3][1]）；再求这两个小区间的最小值，然后再求大区间的最小值。然后以此规律迭代进行求解。

由上面分析有，我们可以得到ST算法求解区间最值问题的状态转移方程是（这里以最小值为例）：

F[i][j] = min(F[i][j-1]，F[i+2j-1][j-1])。（j<=log2n ，n为元素的总个数）

而初始状态为：F[i][0]=a[i]；

代码实现
1
2
3
4
5
//变量说明，下同。
public static int maxd = 50000+7;
public static int[] a = new int[maxd]; //原数组
public static int[][] mina = new int[maxd][110]; //存区间最小值
public static int[][] maxa = new int[maxd][110]; //存区间最大值
1
2
3
4
5
6
7
8
9
10
11
12
public static void getST(int n){ //n为元素的总个数
    for(int i=1;i<=n;++i){
        mina[i][0]=a[i]; 
        maxa[i][0]=a[i];
    }
    for(int j=1;j<=log(n);++j){ //2的j次方。也可以写为 （1<<j）<=n
        for(int i= 1; i+(1<<j)-1<=n;++i){ //防止越界
            mina[i][j]=Math.min(mina[i][j-1],mina[i+(1<<(j-1))][j-1]); //最小值
            maxa[i][j]=Math.max(maxa[i][j-1],maxa[i+(1<<(j-1))][j-1]); //最大值
        }
    }
}

查询思路

在处理好的F数组中，每一个状态对应的区间长度都为2i。但是，一般在查询阶段，给出的待查询区间的长度不一定恰好为2i，因此我们需要对查询区间进行处理。处理的办法也是将大区间分成两个小区间。

处理原则是将给定的待查询区间分成满足如下条件的两个小区间：

  • 两个小区间能覆盖整个区间。
  • 为了利用预处理阶段的结果，要求两个小区间长度相等且都为2t（两个小区间可能重叠）

其中，若待查询区间为【L，R】，则上步中的 t = int(log2(R-L+1))，即 t 等于对区间长度取以2为底的对数。

显然，待查区间【L，R】可以分成两个小区间【L，L+2t-1】和【R-2t+1，R】，他们分别对应 F[L][t] 和 F[R-2t+1][t]，很显然，这两个小区间是把大区间覆盖完了的，如图。

然后，只需要求出这两个小区间的最值，就能求出大区间的最值。

代码实现
1
2
3
4
5
6
7
8
public static int ST_minQuery(int l,int r ){ //查询区间最小值
    int t = log(r-l+1); //r-l+1表示区间的长度
    return Math.min(mina[l][t],mina[r-(1<<t)+1][t]);
}
public static int ST_maxQuery(int l,int r ){ //查询区间最大值
    int t = log(r-l+1);
    return Math.max(maxa[l][t],maxa[r-(1<<t)+1][t]);
}

代码实现

题目练习1

题目练习2

代码以练习2实现，因为把最大最小都求了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
import java.io.*;
import java.math.BigInteger;
import java.util.*;


/**
 * @Author DragonOne
 * @Date 2021/12/5 21:27
 * @墨水记忆 www.tothefor.com
 */
public class Main {
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    public static StreamTokenizer cin = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter cout = new PrintWriter(new OutputStreamWriter(System.out));
    public static Scanner sc = new Scanner(System.in);

    public static int maxd = 50000+7;
    public static int INF = 0x3f3f3f3f;
    public static int mod = 998244353;
    public static int[] a = new int[maxd];
    public static int[][] mina = new int[maxd][110]; //存区间最小值
    public static int[][] maxa = new int[maxd][110]; //存区间最大值

    public static void getST(int n){
        for(int i=1;i<=n;++i){
            mina[i][0]=a[i];
            maxa[i][0]=a[i];
        }
        for(int j=1;j<=log(n);++j){ //2的j次方。也可以写为 （1<<j）<=n
            for(int i= 1; i+(1<<j)-1<=n;++i){ //防止越界
                mina[i][j]=Math.min(mina[i][j-1],mina[i+(1<<(j-1))][j-1]);
                maxa[i][j]=Math.max(maxa[i][j-1],maxa[i+(1<<(j-1))][j-1]);
            }
        }
    }
    public static int ST_minQuery(int l,int r ){ //查询区间最小值
        int t = log(r-l+1);
        return Math.min(mina[l][t],mina[r-(1<<t)+1][t]);
    }
    public static int ST_maxQuery(int l,int r ){ //查询区间最大值
        int t = log(r-l+1);
        return Math.max(maxa[l][t],maxa[r-(1<<t)+1][t]);
    }

    public static void main(String[] args) throws Exception {

        int n = nextInt();
        int q = nextInt();
        for(int i=1;i<=n;++i) a[i]=nextInt();
        getST(n);
        while(q-->0){
            int l = nextInt();
            int r = nextInt();
            cout.println(ST_maxQuery(l,r)-ST_minQuery(l,r));
            cout.flush();
        }

        closeAll();
    }

    public static void cinInit(){
        cin.wordChars('a', 'z');
        cin.wordChars('A', 'Z');
        cin.wordChars(128 + 32, 255);
        cin.whitespaceChars(0, ' ');
        cin.commentChar('/');
        cin.quoteChar('"');
        cin.quoteChar('\'');
        cin.parseNumbers(); //可单独使用来还原数字
    }

    public static int log(int x){ //log方法是以2为底,求x的对数。java自带的log是以e为底的
        return (int) (Math.log(x)/Math.log(2));
    }

    public static int nextInt() throws Exception{
        cin.nextToken();
        return (int) cin.nval;
    }
    public static long nextLong() throws Exception{
        cin.nextToken();
        return (long) cin.nval;
    }
    public static double nextDouble() throws Exception{
        cin.nextToken();
        return cin.nval;
    }
    public static String nextString() throws Exception{
        cin.nextToken();
        return cin.sval;
    }
    public static void closeAll() throws Exception {
        cout.close();
        in.close();
        out.close();
    }

}